| DrJez Home Page |
| Chemistry for Engineers |
| Introductory Physical Chem |
| Physical Chemistry II |
| Office and Teaching Schedule |
| Lab Assisting |
| E-mail Contact |
|
From Dartmouth College Natural Clocks: Cricket chirps There are several natural phenomena - the rate ants walk, the rate fireflies flash, the rate of a terrapin's heartbeat, and even the frequency of human alpha brain-wave patterns - that follow the Arrhenius equation closely. This page looks at one well-studied case, the chirp rate of the snowy tree cricket, oecanthus fultoni. This little cricket, shown below, is familiar to outdoor enthusiasts as a chirping thermometer. (It is found in every US state except Hawaii, Alaska, Montana, and Florida.) That's him (or her - I can't tell) you hear (or just heard) chirping now.
Outside magazine, in its June, 1995, issue,
had a story on this cricket's thermometric ability. They
state, "snowy tree crickets are more accurate than most
[cricket species]; their chirps are slow enough to
count, and they synchronize their singing."
Here's a
site with a series of recorded chirps at various
temperatures. If you turn those recordings into sound
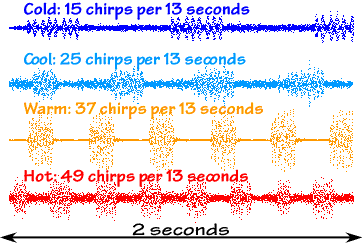
intensity versus time graphs, you can see each
individual chirp and immediately see how the chirp rate
(and even each individual chirp) varies with
temperature:
Outside says, "Count the chirps over a 13-second
period and add 40. That'll give the temperature in
degrees Fahrenheit, give or take a bit." The University
of California Extension, however, has a more complicated
formula: "Count the chirps per minute, subtract 40,
divide by 4, add 50 and that will be the temperature in
degrees Fahrenheit." On the other hand,
The Columbia Encyclopedia, Fifth Edition, says. "If
the number 40 is added to the number of chirps per
15-sec interval, the sum is a fair approximation of the
temperature in degrees Fahrenheit." (It looks like the
good folks at the UC Extension just like to take a
simple formula and make it obscure; their long-winded
rule is the same as Columbia's!) So while Mr. Cricket
clearly chirps with a temperature-dependent rate, there
seems to be some disagreement as to how to interpret it.
What does Arrhenius say? First, the Arrhenius equation is a fairly complicated function of temperature. It says the rate depends on the exponential of a constant quantity, –Ea/R, divided by the absolute temperature. The cricketeers propose a simple linear rate expression (where I've used the Outside magazine 13 second formula, which gives a better fit than the 15 second rule):
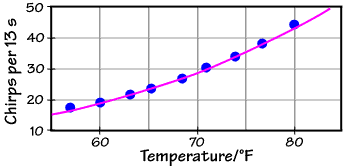
T/°F = (# chirps per 13 seconds) + 40 or Rate = Chirps per 13 seconds = T/°F – 40 Here are some actual data, taken around 1900 and converted to our units:
The empirical formula (the red line) does a reasonable job (and is certainly easier to use than the Arrhenius formula when you're in the great outdoors without your scientific calculator), but there is clearly a curvature to the actual data which a linear formula can't reproduce. If we fit these data to the Arrhenius equation, however, we get the graph below:
This fit, the purple line,
does a better job over the full temperature range (which
spans only 13 K -- living things don't do well over
extremely wide ranges of absolute temperature). What's
more, it tells us something about the undoubtedly
complicated, coupled, and largely unknown set of
chemical reactions that generates the chirp in the first
place: the effective activation energy. If this number
turns out to be a chemically reasonable one (something
on the order of a few to a few tens of kJ mol–1),
then we can have confidence that our physical
interpretation of the chirping mechanism is correct.
The fit equation shown above is: Chirps per 13 seconds = 5.63 x 1010 exp[–(6290 K) / T ] Note the parameter in the exponential: –6290 K, a quantity with units of absolute temperature. This parameter must equal –Ea/R, and with R = 8.31 J mol–1 K–1, we find Ea = 52 kJ mol–1, a very reasonable number!
|
| |